Biorąc pod uwagę liczbę dodatnią , znajdź liczbę alkanów o atomach węgla, ignorując stereoizomery ; lub równoważnie, liczba nieoznakowanych drzew z węzłami, tak że każdy węzeł ma stopień .
Jest to sekwencja OEIS A000602 .
Zobacz także: Parafiny - kod Rosetty
Przykład
Dla odpowiedź wynosi , ponieważ heptan ma dziewięć izomerów :
- Heptan :

- 2-metyloheksan :

- 3-metyloheksan :

- 2,2-dimetylopentan :

- 2,3-dimetylopentan :

- 2,4-dimetylopentan :

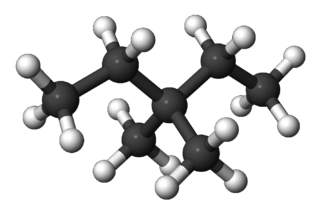


Należy zauważyć, że 3-metyloheksan i 2,3-dimetylopentan są chiralne , ale tutaj ignorujemy stereoizomery.
Przypadki testowe
intput output
=============
0 1
1 1
2 1
3 1
4 2
5 3
6 5
7 9
8 18
9 35
10 75
11 159
12 355
13 802
14 1858
15 4347
16 10359
17 24894
18 60523
19 148284
20 366319
code-golf
sequence
combinatorics
chemistry
alephalpha
źródło
źródło

Odpowiedzi:
CJam (
100 98 91 8983 bajtów)Pobiera dane wejściowe ze standardowego wejścia, a wyjściowe na standardowe wyjście. Zauważ, że wykorzystuje to licencję do nieobsługiwania danych wejściowych w
0celu zaoszczędzenia dwóch bajtów poprzez wstawienie definicjiCiD. Demo onlineUwaga: jest to bardzo wolne i nieefektywne pod względem pamięci. Przycinanie tablic pozwala uzyskać znacznie szybszą wersję (3 bajty więcej). Demo online .
Sekcja
Zmanipulowałem to do rozkładu nieco bardziej golfistycznego, a następnie przejrzałem sekwencje pośrednie i odkryłem, że są one również w OEIS:
Wcześniejsze wersje ponownie wykorzystywały blok
C(zwijają dwa wielomiany) z tej odpowiedzi . Znalazłem o wiele krótszy, ale nie mogę zaktualizować tej odpowiedzi, ponieważ pochodzi ona z łańcuchowego pytania.źródło
Node.js 11.6.0 ,
229 223 221218 bajtówPochodzi z implementacji Java sugerowanej w kodzie Rosetta .
Wypróbuj online!
źródło
Alchemik (1547 bajtów)
Demo online .
Uwaga: jest to dość powolne. Jeśli testowanie za pomocą interpretera, który obsługuje wielokrotne stosowanie reguły jednocześnie (np. Mojej - chociaż upewnij się, że masz najnowszą wersję, która naprawia błąd w parserze), możesz uzyskać znaczne przyspieszenie, dodając dwie reguły:
które wyznaczają trasę według istniejących reguł
Częściowe rozwarstwienie
Na wysokim poziomie używa tego samego podejścia, co moja odpowiedź CJam.
Model obliczeniowy Alchemist jest zasadniczo maszyną rejestru Minsky'ego . Jednak Alchemist bardzo ładnie ujawnia równoważność kodu i danych, a pozwalając skutecznie na wiele tokenów po lewej stronie reguły produkcji, stan nie jest ograniczony do reprezentowania przez jeden atom: możemy użyć krotki atomów, a to zezwala na (nierekurencyjne) podprogramy. Jest to bardzo przydatne w golfa. Jedyne, czego tak naprawdę brakuje, to makra i możliwość debuggowania.
Pebnbebtdedrozwija się do co najmniej 17 bajtów:
gdzie
Sjest obecny stan iTnastępny. Nieniszcząca „kopia” jest jeszcze droższa, ponieważ musi być wykonana jako „ruch” zadobi pomocniczytmp, a następnie „ruch” ztmppowrotem doa.Zaciemnianie
Zróżnicowałem różne zmienne i wyeliminowałem około 60 stanów w trakcie gry w golfa w programie, a wiele z nich i tak nie miało szczególnie znaczących nazw, ale aby w pełni zagrać w golfa, napisałem minimiser, więc nazwy są teraz całkowicie nieczytelne. Powodzenia inżynieria odwrotna! Oto minimalizator (w CJam), który przyjmuje kilka założeń dotyczących kodu, ale można go dostosować w celu zminimalizowania innych programów Alchemist:
źródło
Pari / GP , 118 bajtów
Bezpośrednie tłumaczenie Peter Taylor „s CJam odpowiedź .
Wypróbuj online!
źródło