Obecnie przygotowuję się do rozmowy kwalifikacyjnej i przypomniało mi to o pytaniu, które zadano mi kiedyś w poprzednim wywiadzie, które wyglądało mniej więcej tak:
„Poproszono Cię o zaprojektowanie oprogramowania do ciągłego wyświetlania 10 najczęściej wyszukiwanych haseł w Google. Otrzymujesz dostęp do źródła, które zapewnia niekończący się strumień wyszukiwanych haseł w czasie rzeczywistym w Google. Opisz, jaki algorytm i struktury danych by to zaimplementować. Masz zaprojektować dwie odmiany:
(i) Wyświetl 10 najpopularniejszych wyszukiwanych haseł wszechczasów (tj. od momentu rozpoczęcia czytania kanału).
(ii) Wyświetla tylko 10 najpopularniejszych wyszukiwanych haseł z ostatniego miesiąca, aktualizowanych co godzinę.
Możesz użyć przybliżenia, aby uzyskać listę 10 najlepszych, ale musisz uzasadnić swoje wybory. ”
Byłem bombardowany w tym wywiadzie i nadal nie mam pojęcia, jak to zaimplementować.
Pierwsza część prosi o 10 najczęściej występujących pozycji w stale rosnącej pod-sekwencji nieskończonej listy. Przyjrzałem się algorytmom selekcji, ale nie mogłem znaleźć żadnych wersji online, aby rozwiązać ten problem.
Druga część wykorzystuje skończoną listę, ale ze względu na dużą ilość przetwarzanych danych nie można tak naprawdę przechowywać w pamięci całego miesiąca wyszukiwanych haseł i co godzinę obliczać histogramu.
Problem utrudnia fakt, że lista 10 najlepszych jest stale aktualizowana, więc musisz w jakiś sposób obliczyć swoją pierwszą 10 w przesuwanym oknie.
Jakieś pomysły?

what is the most frequent item in the subsequence [2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5] of your sequence?Odpowiedzi:
Cóż, wygląda na to, że jest bardzo dużo danych, a przechowywanie wszystkich częstotliwości może być zbyt kosztowne. Gdy ilość danych jest tak duża, że nie możemy liczyć na ich przechowywanie, wchodzimy w dziedzinę algorytmów strumienia danych .
Przydatna książka w tej dziedzinie: Muthukrishnan - „Strumienie danych: algorytmy i aplikacje”
Ściśle powiązane odniesienie do problemu, który wybrałem z powyższego: Manku, Motwani - "Przybliżone liczniki częstotliwości w strumieniach danych" [pdf]
Nawiasem mówiąc, Motwani ze Stanford (edytuj) był autorem bardzo ważnej książki „Randomized Algorithms” .
Problem ten dotyczy jedenastego rozdziału tej książki. Edycja: Przepraszamy, kiepskie odniesienie, ten rozdział dotyczy innego problemu. Po sprawdzeniu, że zamiast polecić punkt 5.1.2 Muthukrishnan za książki , dostępne on-line.Hej, miłe pytanie do wywiadu.
źródło
Przegląd szacowania częstotliwości
Istnieje kilka dobrze znanych algorytmów, które mogą zapewnić oszacowania częstotliwości dla takiego strumienia przy użyciu stałej ilości pamięci. One is Frequent, autorstwa Misra i Gries (1982). Z listy n elementów wyszukuje wszystkie elementy, które występują więcej niż n / k razy, używając liczników k - 1 . Jest to uogólnienie algorytmu większości Boyera i Moore'a (Fischer-Salzberg, 1982), gdzie k wynosi 2. Algorytmy Manku i Motwani's LossyCounting (2002) oraz Metwally 's SpaceSaving (2005) mają podobne wymagania przestrzenne, ale mogą zapewnić dokładniejsze szacunki pod pewnymi warunki.
Ważną rzeczą do zapamiętania jest to, że te algorytmy mogą dostarczać tylko oszacowania częstotliwości. W szczególności oszacowanie Misra-Gries może zaniżać rzeczywistą częstotliwość o (n / k) pozycji.
Załóżmy, że masz algorytm, który może pozytywnie zidentyfikować element tylko wtedy, gdy występuje on w ponad 50% przypadków. Podaj temu algorytmowi strumień N różnych elementów, a następnie dodaj kolejne N - 1 kopii jednego elementu, x , w sumie 2N - 1 elementów. Jeśli algorytm mówi ci, że x przekracza 50% całości, to musiało być w pierwszym strumieniu; jeśli tak nie jest, x nie było w początkowym strumieniu. Aby algorytm mógł to określić, musi przechowywać strumień początkowy (lub jakieś podsumowanie proporcjonalne do jego długości)! Możemy więc sobie udowodnić, że przestrzeń wymagana przez taki „dokładny” algorytm wynosiłaby Ω ( N ).
Zamiast tego opisane tutaj algorytmy częstotliwości zapewniają oszacowanie, identyfikując każdy element, który przekracza próg, wraz z niektórymi elementami, które spadają poniżej niego o pewien margines. Na przykład algorytm większości , wykorzystujący pojedynczy licznik, zawsze da wynik; jeśli jakikolwiek element przekroczy 50% strumienia, zostanie znaleziony. Ale może również dać ci przedmiot, który występuje tylko raz. Nie wiedziałbyś bez drugiego przejścia przez dane (znowu używając pojedynczego licznika, ale szukając tylko tego elementu).
Częsty algorytm
Oto prosty opis algorytmu Częsty Misra-Gries . Demaine (2002) i inni zoptymalizowali algorytm, ale to daje ci sedno.
Określ ułamek progowy, 1 / k ; każdy element, który wystąpi więcej niż n / k razy, zostanie znaleziony. Utwórz pustą mapę (jak czerwono-czarne drzewo); klucze będą wyszukiwanymi hasłami, a wartości będą licznikiem dla tego terminu.
Zwróć uwagę, że możesz przetwarzać nieskończoną ilość danych przy stałej ilości pamięci (tylko mapa o stałym rozmiarze). Wymagana ilość pamięci zależy tylko od progu zainteresowania, a wielkość strumienia nie ma znaczenia.
Liczenie wyszukiwań
W tym kontekście być może buforujesz godzinę wyszukiwań i wykonujesz ten proces na danych z tej godziny. Jeśli możesz wziąć drugi przebieg w dzienniku wyszukiwania z tej godziny, możesz uzyskać dokładną liczbę wystąpień najlepszych „kandydatów” zidentyfikowanych w pierwszym przebiegu. A może w porządku jest zrobić jedno przejście i zgłosić wszystkich kandydatów, wiedząc, że każdy przedmiot, który powinien się tam znaleźć, jest uwzględniony, a wszelkie dodatki to tylko hałas, który zniknie w ciągu następnej godziny.
Wszyscy kandydaci, którzy rzeczywiście przekraczają próg zainteresowania, są zapisywani jako podsumowanie. Przechowuj te podsumowania z miesiąca, wyrzucaj najstarsze co godzinę, a uzyskasz dobre przybliżenie najczęściej wyszukiwanych haseł.
źródło
To jeden z projektów badawczych, przez które obecnie przechodzę. Wymagania są prawie takie same, jak Twoje, a my opracowaliśmy ładne algorytmy do rozwiązania problemu.
Wejście
Dane wejściowe to niekończący się strumień angielskich słów lub zwrotów (nazywamy je
tokens).Wyjście
Zastosowanie tego badania polega na znalezieniu gorącego tematu lub trendów na Twitterze lub Facebooku. Mamy robota indeksującego stronę internetową, który generuje strumień słów, które zostaną wprowadzone do systemu. System następnie wypisze słowa lub frazy o najwyższej częstotliwości, ogólnie lub historycznie. Wyobraź sobie, że w ciągu ostatnich kilku tygodni na Twitterze wielokrotnie pojawiało się hasło „Mistrzostwa Świata”. Tak samo jak „Paul the Octopus”. :)
Ciąg na liczby całkowite
System posiada całkowity identyfikator dla każdego słowa. Chociaż w Internecie jest prawie nieskończenie wiele możliwych słów, to po zgromadzeniu dużego zestawu słów możliwość znalezienia nowych słów staje się coraz mniejsza. Znaleźliśmy już 4 miliony różnych słów i do każdego przypisaliśmy unikalny identyfikator. Cały zestaw danych można załadować do pamięci jako tablicę mieszającą, zajmującą około 300 MB pamięci. (Zaimplementowaliśmy własną tablicę mieszającą. Implementacja języka Java wymaga ogromnej ilości pamięci)
Następnie każdą frazę można zidentyfikować jako tablicę liczb całkowitych.
Jest to ważne, ponieważ sortowanie i porównywanie liczb całkowitych jest znacznie szybsze niż na łańcuchach.
Archiwizuj dane
System przechowuje dane archiwalne dla każdego tokena. Zasadniczo to pary
(Token, Frequency). Jednak tabela przechowująca dane byłaby tak ogromna, że musielibyśmy fizycznie podzielić tabelę. Raz schemat partycji jest oparty na ngramach tokenu. Jeśli token jest pojedynczym słowem, jest to 1 gram. Jeśli token jest frazą składającą się z dwóch słów, jest to 2 gramy. I to trwa. Przy przybliżeniu przy 4 gramach mamy 1 miliard rekordów, a rozmiar tabeli wynosi około 60 GB.Przetwarzanie strumieni przychodzących
System będzie wchłaniał nadchodzące zdania, dopóki pamięć nie zostanie w pełni wykorzystana (tak, potrzebujemy MemoryManagera). Po pobraniu N zdań i zapisaniu ich w pamięci, system zatrzymuje się i zaczyna tokenizować każde zdanie na słowa i frazy. Każdy token (słowo lub fraza) jest liczony.
W przypadku bardzo częstych żetonów są one zawsze przechowywane w pamięci. W przypadku rzadszych tokenów są one sortowane na podstawie identyfikatorów (pamiętaj, że tłumaczymy String na tablicę liczb całkowitych) i serializowane do pliku na dysku.
(Jednak dla twojego problemu, ponieważ liczysz tylko słowa, możesz umieścić całą mapę częstotliwości słów tylko w pamięci. Starannie zaprojektowana struktura danych zajmie tylko 300 MB pamięci na 4 miliony różnych słów. Wskazówka: użyj znaku ASCII, aby reprezentują ciągi znaków) i jest to bardzo akceptowalne.
W międzyczasie, po znalezieniu dowolnego pliku dyskowego wygenerowanego przez system, aktywowany zostanie inny proces, a następnie rozpocznie się scalanie. Ponieważ plik na dysku jest posortowany, scalanie wymagałoby podobnego procesu, jak sortowanie przez scalanie. Tutaj również należy zadbać o niektóre projekty, ponieważ chcemy uniknąć zbyt wielu przypadkowych wyszukiwań dysku. Chodzi o to, aby uniknąć odczytu (procesu scalania) / zapisu (wyjście systemowe) w tym samym czasie i pozwolić procesowi scalania na odczyt z jednego dysku podczas zapisywania na innym dysku. Jest to podobne do wdrażania blokady.
Koniec dnia
Pod koniec dnia system będzie miał wiele częstych tokenów z częstotliwością przechowywanych w pamięci oraz wiele innych rzadziej używanych tokenów przechowywanych w kilku plikach dyskowych (a każdy plik jest posortowany).
System opróżnia mapę w pamięci do pliku dyskowego (sortuje ją). Teraz problemem staje się scalanie zestawu posortowanych plików dyskowych. Korzystając z podobnego procesu, otrzymalibyśmy na końcu jeden posortowany plik na dysku.
Następnie ostatnim zadaniem jest scalenie posortowanego pliku dyskowego z bazą danych archiwum. W zależności od wielkości bazy danych archiwum algorytm działa jak poniżej, jeśli jest wystarczająco duży:
Intuicja jest taka, że po pewnym czasie liczba włożeń będzie coraz mniejsza. Coraz więcej operacji będzie dotyczyło tylko aktualizacji. A ta aktualizacja nie będzie karana indeksem.
Mam nadzieję, że całe to wyjaśnienie pomoże. :)
źródło
Możesz użyć tablicy mieszającej w połączeniu z binarnym drzewem wyszukiwania . Zaimplementuj
<search term, count>słownik, który powie Ci, ile razy każde wyszukiwane hasło było wyszukiwane.Oczywiście iterowanie całej tabeli haszowania co godzinę w celu uzyskania pierwszej dziesiątki jest bardzo złe. Ale to jest Google, o którym mówimy, więc można założyć, że pierwsza dziesiątka otrzyma, powiedzmy, ponad 10 000 odsłon (to jednak prawdopodobnie znacznie większa liczba). Dlatego za każdym razem, gdy liczba wyszukiwanego hasła przekracza 10 000, wstaw ją do BST. Następnie co godzinę wystarczy pobrać pierwsze 10 z BST, które powinno zawierać stosunkowo niewiele wpisów.
To rozwiązuje problem pierwszej dziesiątki wszech czasów.
Naprawdę trudna część polega na tym, że jeden termin zajmuje miejsce innego w raporcie miesięcznym (na przykład „przepełnienie stosu” może mieć 50 000 trafień w ciągu ostatnich dwóch miesięcy, ale tylko 10 000 w ostatnim miesiącu, podczas gdy „amazon” może mieć 40 000 za ostatnie dwa miesiące, ale 30 000 za ostatni miesiąc. Chcesz, aby w raporcie miesięcznym „amazon” znajdował się przed „przepełnieniem stosu”). Aby to zrobić, zapisałbym dla wszystkich głównych (powyżej 10 000 wyszukiwań wszech czasów) 30-dniową listę, która zawiera informacje o tym, ile razy dane hasło było wyszukiwane każdego dnia. Lista działałaby jak kolejka FIFO: usuwasz pierwszy dzień i wstawiasz nowy każdego dnia (lub co godzinę, ale wtedy może być konieczne przechowywanie większej ilości informacji, co oznacza więcej pamięci / miejsca. Jeśli pamięć nie jest problemem, zrób to) to, w przeciwnym razie wybierz to „przybliżenie”
To wygląda na dobry początek. Możesz wtedy martwić się o przycinanie terminów, które mają> 10 000 trafień, ale od dawna nie mają ich zbyt wiele i tego typu rzeczy.
źródło
przypadek i)
Utrzymuj tablicę hashtagów dla wszystkich terminów wyszukiwania, a także posortowaną listę dziesięciu pierwszych pozycji, oddzieloną od tablicy hashy. Za każdym razem, gdy nastąpi wyszukiwanie, zwiększ odpowiednią pozycję w tablicy hashy i sprawdź, czy ta pozycja powinna zostać teraz zamieniona na dziesiątą pozycję na liście dziesięciu pierwszych.
O (1) wyszukiwanie listy dziesięciu pierwszych i maksymalne wstawienie O (log (n)) do tablicy hashy (przy założeniu, że kolizje są zarządzane przez samo równoważące się drzewo binarne).
przypadek ii) Zamiast utrzymywać ogromną tablicę haszującą i małą listę, utrzymujemy tablicę haszy i posortowaną listę wszystkich elementów. Za każdym razem, gdy wykonywane jest wyszukiwanie, termin ten jest zwiększany w tablicy hashy, a na posortowanej liście można sprawdzić, czy termin powinien zamienić się z terminem po nim. Równoważące się drzewo binarne może się do tego dobrze przydać, ponieważ musimy również mieć możliwość szybkiego odpytywania go (więcej o tym później).
Dodatkowo prowadzimy również listę „godzin” w postaci listy FIFO (kolejki). Każdy element „godzina” zawierałby listę wszystkich wyszukiwań przeprowadzonych w tej konkretnej godzinie. Na przykład nasza lista godzin może wyglądać następująco:
Następnie co godzinę: jeśli lista ma co najmniej 720 godzin (to jest liczba godzin w ciągu 30 dni), spójrz na pierwszy element na liście i dla każdego wyszukiwanego hasła zmniejsz ten element w tablicy hashy o odpowiednią wartość . Następnie usuń ten element pierwszej godziny z listy.
Powiedzmy, że jesteśmy w godzinie 721 i jesteśmy gotowi spojrzeć na pierwszą godzinę na naszej liście (powyżej). Zmniejszylibyśmy liczbę darmowych rzeczy o 56 w hashtagach, zabawnych zdjęciach o 321 itd., A następnie całkowicie usunęlibyśmy godzinę 0 z listy, ponieważ nigdy nie będziemy musieli więcej na nią patrzeć.
Powodem, dla którego utrzymujemy posortowaną listę wszystkich terminów, która pozwala na szybkie zapytania, jest to, że co godzinę, przeglądając wyszukiwane hasła sprzed 720 godzin, musimy upewnić się, że lista dziesięciu najlepszych pozostaje posortowana. Tak więc, na przykład, zmniejszając liczbę „darmowych rzeczy” o 56 w tablicy hashy, sprawdzalibyśmy, gdzie teraz należy do listy. Ponieważ jest to samo-równoważące się drzewo binarne, wszystko to można ładnie wykonać w czasie O (log (n)).
Edycja: Poświęcanie dokładności dla kosmosu ...
Przydałoby się również zaimplementować dużą listę w pierwszej, podobnie jak w drugiej. Następnie możemy zastosować następującą optymalizację przestrzeni w obu przypadkach: Uruchom zadanie cron, aby usunąć wszystkie elementy z listy oprócz najwyższych x . Zmniejszyłoby to zapotrzebowanie na miejsce (iw rezultacie przyspieszyło zapytania na liście). Oczywiście dałoby to przybliżony wynik, ale jest to dozwolone. x można obliczyć przed wdrożeniem aplikacji na podstawie dostępnej pamięci i dostosowywać dynamicznie, jeśli będzie dostępne więcej pamięci.
źródło
Nieostrożne myślenie ...
W pierwszej dziesiątce wszechczasów
Top 10 miesięcznych aktualizowanych co godzinę:
Errr ... ma sens? Nie przemyślałem tego tak, jak w prawdziwym życiu
Ach tak, zapomniałem wspomnieć, że godzinowe „kopiowanie / spłaszczanie” wymagane w miesięcznych statystykach może w rzeczywistości ponownie wykorzystać ten sam kod, co 10 najlepszych wszech czasów, co jest miłym efektem ubocznym.
źródło
Dokładne rozwiązanie
Po pierwsze rozwiązanie, które gwarantuje poprawne wyniki, ale wymaga dużej ilości pamięci (duża mapa).
Wariant „wszechczasów”
Utrzymuj mapę skrótów z zapytaniami jako kluczami i ich liczbą jako wartościami. Dodatkowo przechowuj listę 10 najczęściej występujących zapytań do tej pory oraz liczbę dziesiątych najczęściej występujących zliczeń (próg).
Stale aktualizuj mapę w miarę odczytywania strumienia zapytań. Za każdym razem, gdy liczba przekracza bieżący próg, wykonaj następujące czynności: usuń dziesiąte zapytanie z listy „Top 10”, zastąp je zapytaniem, które właśnie zaktualizowałeś, a także zaktualizuj próg.
Wariant „Ostatni miesiąc”
Zachowaj tę samą listę „Top 10” i zaktualizuj ją w taki sam sposób, jak powyżej. Zachowaj również podobną mapę, ale tym razem przechowuj wektory o liczbie 30 * 24 = 720 (jeden na każdą godzinę) jako wartości. Co godzinę wykonaj następujące czynności dla każdego klucza: usuń najstarszy licznik z wektora dodaj nowy (zainicjowany na 0) na końcu. Usuń klucz z mapy, jeśli wektor jest zerowy. Ponadto co godzinę musisz od nowa obliczyć listę „Top 10”.
Uwaga: tak, tym razem przechowujemy 720 liczb całkowitych zamiast jednej, ale jest znacznie mniej kluczy (wariant wszechczasów ma naprawdę długi ogon).
Przybliżenia
Te przybliżenia nie gwarantują poprawnego rozwiązania, ale zużywają mniej pamięci.
źródło
10 najczęściej wyszukiwanych haseł z ostatniego miesiąca
Korzystanie z wydajnego pamięciowo indeksowania / struktury danych, takiej jak ciasno upakowane próby (z wpisów Wikipedii na temat prób ), w przybliżeniu definiuje pewien związek między wymaganiami pamięci a n - liczbą terminów.
W przypadku, gdy wymagana pamięć jest dostępna ( założenie 1 ), możesz zachować dokładne miesięczne statystyki i agregować je co miesiąc w statystykę wszechczasów.
Istnieje tu również założenie, które interpretuje „ostatni miesiąc” jako stałe okno. Ale nawet jeśli okno miesięczne przesuwa się, powyższa procedura działa na zasadzie (przesuwanie można w przybliżeniu przyrównać do stałych okien o danej wielkości).
To przypomina mi bazę danych z działaniem okrężnym z wyjątkiem tego, że niektóre statystyki są obliczane na zasadzie „all time” (w pewnym sensie, że nie wszystkie dane są zachowane; rrd konsoliduje okresy z pominięciem szczegółów poprzez uśrednianie, sumowanie lub wybieranie wartości max / min, w danym zadaniu tracone są informacje o elementach o niskiej częstotliwości, które mogą wprowadzać błędy).
Założenie 1
Jeśli nie możemy utrzymać doskonałych statystyk przez cały miesiąc, powinniśmy być w stanie znaleźć pewien okres P, dla którego powinniśmy być w stanie utrzymać doskonałe statystyki. Na przykład, zakładając, że mamy doskonałe statystyki dotyczące pewnego okresu P, który przechodzi w miesiąc n razy.
Doskonałe statystyki definiują funkcję
f(search_term) -> search_term_occurance.Jeśli uda nam się zachować
nw pamięci wszystkie idealne tabele statystyk, miesięczne statystyki przesuwne można obliczyć w następujący sposób:ndoskonałe tabele statystyk)Jeśli jednak utrzymamy tylko top 10 na poziomie zagregowanym (miesięcznym), będziemy mogli odrzucić wiele danych z pełnych statystyk z ustalonego okresu. Daje to już działającą procedurę, która ma ustalone (przy założeniu górnej granicy idealnej tabeli statystyk dla okresu P) wymagania dotyczące pamięci.
Problem z powyższą procedurą polega na tym, że jeśli przechowujemy informacje tylko o 10 najważniejszych terminach dla przesuwanego okna (podobnie przez cały czas), to statystyki będą poprawne dla wyszukiwanych haseł, które osiągają szczyt w okresie, ale mogą nie widzieć statystyki wyszukiwanych haseł, które pojawiają się stale w czasie.
Można to zrównoważyć, przechowując informacje na temat więcej niż 10 najważniejszych terminów, na przykład 100 najlepszych, mając nadzieję, że 10 najlepszych będzie poprawnych.
Myślę, że dalsza analiza mogłaby odnosić się do minimalnej liczby wystąpień wymaganych, aby wpis stał się częścią statystyk (co jest związane z maksymalnym błędem).
(Decydując, które wpisy powinny stać się częścią statystyk, można również monitorować i śledzić trendy; na przykład, jeśli liniowa ekstrapolacja zdarzeń w każdym okresie P dla każdego terminu mówi, że termin stanie się znaczący za miesiąc lub dwa, może już rozpocząć śledzenie. Podobna zasada ma zastosowanie do usuwania wyszukiwanego hasła ze śledzonej puli).
Najgorszym przypadkiem powyższego jest sytuacja, w której masz wiele prawie równie częstych haseł i zmieniają się one cały czas (na przykład jeśli śledzisz tylko 100 terminów, to jeśli 150 najlepszych terminów występuje równie często, ale 50 najlepszych jest częściej w pierwszym miesiącu) i by często po jakimś czasie statystyki nie były prowadzone poprawnie).
Mogłoby też istnieć inne podejście, które nie jest ustalone pod względem wielkości pamięci (ściśle mówiąc też nie jest to powyższe), które definiowałoby minimalne znaczenie w kategoriach zdarzeń / okresu (dzień, miesiąc, rok, cały czas), dla których należy zachować statystyki. Może to zagwarantować maksymalny błąd w każdej ze statystyk podczas agregacji (zobacz ponownie okrężny).
źródło
A co z adaptacją „algorytmu zastępowania strony zegara” (znanego również jako „druga szansa”)? Mogę sobie wyobrazić, że działa to bardzo dobrze, jeśli żądania wyszukiwania są rozłożone równomiernie (oznacza to, że większość wyszukiwanych haseł pojawia się regularnie, a nie 5 milionów razy z rzędu, a potem nigdy więcej).
Oto wizualna reprezentacja algorytmu: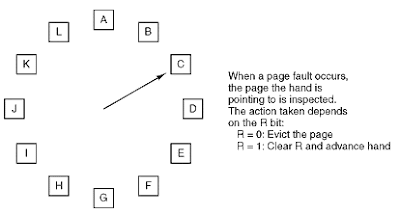
źródło
Przechowuj liczbę wyszukiwanych haseł w gigantycznej tabeli skrótów, w której każde nowe wyszukiwanie powoduje zwiększenie określonego elementu o jeden. Śledź około 20 najczęściej wyszukiwanych haseł; gdy element na 11. miejscu jest zwiększany, sprawdź, czy musi zamienić się pozycjami z # 10 * (nie jest konieczne sortowanie pierwszej dziesiątki; wszystko, co Cię obchodzi, to rozróżnienie między 10 a 11).
* Podobne kontrole muszą zostać przeprowadzone, aby zobaczyć, czy nowe wyszukiwane hasło znajduje się na 11. miejscu, więc ten algorytm przechodzi również do innych wyszukiwanych haseł - więc trochę upraszczam.
źródło
czasami najlepszą odpowiedzią jest „nie wiem”.
Zrobię głębsze dźgnięcie. Moim pierwszym odruchem byłoby przekazanie wyników do pytania Q. Proces nieustannie przetwarzałby elementy wchodzące do Q. Proces utrzymywałby mapę
termin -> liczba
za każdym razem, gdy element Q jest przetwarzany, wystarczy wyszukać wyszukiwany termin i zwiększyć liczbę.
Jednocześnie prowadziłbym listę odniesień do 10 najlepszych wpisów na mapie.
W przypadku wpisu, który był aktualnie zaimplementowany, sprawdź, czy jego liczba jest większa niż liczba najmniejszych wpisów w pierwszej dziesiątce (jeśli nie znajduje się już na liście). Jeśli tak, zastąp najmniejszy wpis.
Myślę, że to zadziała. Żadna operacja nie jest czasochłonna. Musiałbyś znaleźć sposób na zarządzanie rozmiarem mapy licznikowej. ale to powinno wystarczyć do udzielenia odpowiedzi na wywiad.
Nie oczekują rozwiązania, które chcą sprawdzić, czy potrafisz pomyśleć. Nie musisz pisać rozwiązania wtedy i tam ....
źródło
queue,Qto litera :).Jednym ze sposobów jest to, że przy każdym wyszukiwaniu zapisujesz wyszukiwane hasło i jego sygnaturę czasową. W ten sposób znalezienie pierwszej dziesiątki dla dowolnego okresu jest po prostu kwestią porównania wszystkich wyszukiwanych haseł w danym okresie.
Algorytm jest prosty, ale wadą byłoby większe zużycie pamięci i czasu.
źródło
A co z używaniem Splay Tree z 10 węzłami? Za każdym razem, gdy próbujesz uzyskać dostęp do wartości (wyszukiwanego hasła), która nie jest zawarta w drzewie, wyrzuć dowolny liść, wstaw zamiast niego wartość i uzyskaj do niej dostęp.
Idea tego jest taka sama, jak w mojej innej odpowiedzi . Przy założeniu, że wyszukiwane hasła są dostępne równomiernie / regularnie, rozwiązanie to powinno działać bardzo dobrze.
edytować
Można również zapisać w drzewie więcej wyszukiwanych haseł (to samo dotyczy rozwiązania, które sugeruję w mojej drugiej odpowiedzi), aby nie usuwać węzła, do którego można uzyskać dostęp w najbliższym czasie. Im więcej wartości się w nim przechowuje, tym lepsze wyniki.
źródło
Nie wiem, czy dobrze to rozumiem, czy nie. Moje rozwiązanie polega na użyciu sterty. Ze względu na 10 najpopularniejszych pozycji wyszukiwania buduję stertę o rozmiarze 10. Następnie aktualizuję tę stertę za pomocą nowego wyszukiwania. Jeśli częstotliwość nowego wyszukiwania jest większa niż góra sterty (Max Heap), zaktualizuj ją. Porzuć ten z najmniejszą częstotliwością.
Ale to, jak obliczyć częstotliwość konkretnego wyszukiwania, będzie liczone na coś innego. Może, jak wszyscy powiedzieli, algorytm strumienia danych ...
źródło
Użyj cm-sketcha do przechowywania liczby wszystkich wyszukiwań od początku, zachowaj minimalną stertę o rozmiarze 10 w pierwszej dziesiątce. Aby uzyskać miesięczny wynik, zachowaj 30 cm-sketch / hash-table i min-heap z nim, każdy początek liczenie i aktualizacja z ostatnich 30, 29 .., 1 dnia. Jako przepustkę dzienną, wyczyść ostatnią i używaj jej jako dnia 1. To samo dla wyniku godzinowego, zachowaj 60 tablic mieszających i sterty min i zacznij liczyć przez ostatnie 60, 59, ... 1 minutę. Jako minuta usuń ostatnią i użyj jej jako minuty 1.
Wynik miesięczny jest dokładny w zakresie 1 dnia, wynik godzinowy jest dokładny w zakresie 1 min
źródło
Problemu nie da się uniwersalnie rozwiązać, gdy masz określoną ilość pamięci i „nieskończony” (myślę, że bardzo duży) strumień tokenów.
Zgrubne wyjaśnienie ...
Aby zobaczyć, dlaczego, rozważ strumień tokenów, który ma określony token (tj. Słowo) T co N tokenów w strumieniu wejściowym.
Załóżmy również, że pamięć może pomieścić odniesienia (identyfikator słowa i liczbę) do maksymalnie M tokenów.
W tych warunkach można skonstruować strumień wejściowy, w którym token T nigdy nie zostanie wykryty, jeśli N jest wystarczająco duży, aby strumień zawierał różne tokeny M między Tami.
Jest to niezależne od szczegółów algorytmu Top-N. Zależy to tylko od limitu M.
Aby zobaczyć, dlaczego tak jest, rozważ strumień przychodzący składający się z grup dwóch identycznych tokenów:
gdzie a i b są ważnymi tokenami, które nie są równe T.
Zwróć uwagę, że w tym strumieniu T pojawia się dwukrotnie dla każdego ai i bi. Jednak rzadko wydaje się, że zostanie wypłukany z systemu.
Zaczynając od pustej pamięci, pierwszy token (T) zajmie miejsce w pamięci (ograniczone przez M). Wtedy a1 zajmie miejsce, aż do a- (M-1), gdy M jest wyczerpane.
Kiedy nadejdzie aM, algorytm musi upuścić jeden symbol, więc niech będzie to T. Następnym symbolem będzie b-1, co spowoduje opróżnienie a-1 itd.
Tak więc T nie pozostanie w pamięci wystarczająco długo, aby zbudować prawdziwą liczbę. Krótko mówiąc, każdy algorytm pominie symbol wystarczająco niskiej częstotliwości lokalnej, ale wysokiej częstotliwości globalnej (na całej długości strumienia).
źródło