Wygeneruj listę wszystkich możliwych permutacji łańcucha

Jak bym zabrał się do wygenerowania listy wszystkich możliwych permutacji łańcucha o długości od x do y, zawierającego zmienną listę znaków.

Każdy język działałby, ale powinien być przenośny.

Można to zrobić na kilka sposobów. Typowe metody wykorzystują rekursję, zapamiętywanie lub programowanie dynamiczne. Podstawowa idea polega na tym, że tworzysz listę wszystkich ciągów o długości 1, a następnie w każdej iteracji, dla wszystkich napisów utworzonych w ostatniej iteracji, dodajesz ten ciąg połączony z każdym znakiem w ciągu osobno. (indeks zmiennej w poniższym kodzie śledzi początek ostatniej i następnej iteracji)

Jakiś pseudokod:

list = originalString.split('')
index = (0,0)
list = [""]
for iteration n in 1 to y:
  index = (index[1], len(list))
  for string s in list.subset(index[0] to end):
    for character c in originalString:
      list.add(s + c)

musiałbyś wtedy usunąć wszystkie ciągi o długości mniejszej niż x, będą to pierwsze (x-1) * len (originalString) wpisy na liście.

Lepiej jest używać cofania

#include <stdio.h>
#include <string.h>

void swap(char *a, char *b) {
    char temp;
    temp = *a;
    *a = *b;
    *b = temp;
}

void print(char *a, int i, int n) {
    int j;
    if(i == n) {
        printf("%s\n", a);
    } else {
        for(j = i; j <= n; j++) {
            swap(a + i, a + j);
            print(a, i + 1, n);
            swap(a + i, a + j);
        }
    }
}

int main(void) {
    char a[100];
    gets(a);
    print(a, 0, strlen(a) - 1);
    return 0;
}

Dostaniesz dużo strun, to na pewno ...

Gdzie x i y to sposób ich definiowania, a r to liczba znaków, z których wybieramy - jeśli dobrze cię rozumiem. Zdecydowanie powinieneś je generować w razie potrzeby i nie robić niechlujstwa i mówić, wygeneruj zestaw mocy, a następnie przefiltruj długość ciągów.

Poniższe zdecydowanie nie są najlepszym sposobem na ich wygenerowanie, ale mimo wszystko jest to interesujące.

Knuth (tom 4, zeszyt 2, 7.2.1.3) mówi nam, że (s, t) -kombinacja jest równoważna s + 1 rzeczy wziętej t naraz z powtórzeniem - kombinacja (s, t) -jest używana przez Knutha to jest równe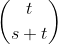 . Możemy to rozgryźć, najpierw generując każdą kombinację (s, t) w postaci binarnej (czyli o długości (s + t)) i zliczając liczbę 0 po lewej stronie każdego 1.

10001000011101 -> staje się permutacją: {0, 3, 4, 4, 4, 1}

Rozwiązanie nierekurencyjne według Knutha, przykład w Pythonie:

def nextPermutation(perm):
    k0 = None
    for i in range(len(perm)-1):
        if perm[i]<perm[i+1]:
            k0=i
    if k0 == None:
        return None

    l0 = k0+1
    for i in range(k0+1, len(perm)):
        if perm[k0] < perm[i]:
            l0 = i

    perm[k0], perm[l0] = perm[l0], perm[k0]
    perm[k0+1:] = reversed(perm[k0+1:])
    return perm

perm=list("12345")
while perm:
    print perm
    perm = nextPermutation(perm)

Możesz spojrzeć na „ Efektywne wyliczanie podzbiorów zbioru ”, które opisuje algorytm, który wykonuje część tego, co chcesz - szybko generuje wszystkie podzbiory N znaków od długości x do y. Zawiera implementację w C.

Dla każdego podzbioru nadal musiałbyś wygenerować wszystkie permutacje. Na przykład, jeśli chcesz mieć 3 znaki z „abcde”, ten algorytm dałby ci „abc”, „abd”, „abe” ... ale musisz permutować każdy z nich, aby uzyskać „acb”, „bac”, „bca” itp.

Część działającego kodu Java w oparciu o odpowiedź Sarpa :

public class permute {

    static void permute(int level, String permuted,
                    boolean used[], String original) {
        int length = original.length();
        if (level == length) {
            System.out.println(permuted);
        } else {
            for (int i = 0; i < length; i++) {
                if (!used[i]) {
                    used[i] = true;
                    permute(level + 1, permuted + original.charAt(i),
                       used, original);
                    used[i] = false;
                }
            }
        }
    }

    public static void main(String[] args) {
        String s = "hello";
        boolean used[] = {false, false, false, false, false};
        permute(0, "", used, s);
    }
}

Oto proste rozwiązanie w C #.

Generuje tylko różne permutacje danego ciągu.

    static public IEnumerable<string> permute(string word)
    {
        if (word.Length > 1)
        {

            char character = word[0];
            foreach (string subPermute in permute(word.Substring(1)))
            {

                for (int index = 0; index <= subPermute.Length; index++)
                {
                    string pre = subPermute.Substring(0, index);
                    string post = subPermute.Substring(index);

                    if (post.Contains(character))
                            continue;                       

                    yield return pre + character + post;
                }

            }
        }
        else
        {
            yield return word;
        }
    }

Jest tu wiele dobrych odpowiedzi. Proponuję również bardzo proste rozwiązanie rekurencyjne w C ++.

#include <string>
#include <iostream>

template<typename Consume>
void permutations(std::string s, Consume consume, std::size_t start = 0) {
    if (start == s.length()) consume(s);
    for (std::size_t i = start; i < s.length(); i++) {
        std::swap(s[start], s[i]);
        permutations(s, consume, start + 1);
    }
}

int main(void) {
    std::string s = "abcd";
    permutations(s, [](std::string s) {
        std::cout << s << std::endl;
    });
}

Uwaga : ciągi z powtarzającymi się znakami nie spowodują unikalnych permutacji.

Właśnie podniosłem to szybko w Rubim:

def perms(x, y, possible_characters)
  all = [""]
  current_array = all.clone
  1.upto(y) { |iteration|
    next_array = []
    current_array.each { |string|
      possible_characters.each { |c|
        value = string + c
        next_array.insert next_array.length, value
        all.insert all.length, value
      }
    }
    current_array = next_array
  }
  all.delete_if { |string| string.length < x }
end

Możesz zajrzeć do API języka dla wbudowanych funkcji typu permutacji i być może będziesz w stanie napisać bardziej zoptymalizowany kod, ale jeśli liczby są aż tak wysokie, nie jestem pewien, czy istnieje wiele sposobów na obejście wielu wyników .

Tak czy inaczej, idea kodu zaczyna się od łańcucha o długości 0, a następnie śledzi wszystkie ciągi o długości Z, gdzie Z jest bieżącym rozmiarem w iteracji. Następnie przejdź przez każdy ciąg i dołącz każdy znak do każdego ciągu. Na koniec usuń wszystko, co było poniżej progu x, i zwróć wynik.

Nie testowałem tego z potencjalnie bezsensownymi danymi wejściowymi (lista znaków zerowych, dziwne wartości x i y itp.).

To jest tłumaczenie wersji Ruby Mike'a na Common Lisp:

(defun perms (x y original-string)
  (loop with all = (list "")
        with current-array = (list "")
        for iteration from 1 to y
        do (loop with next-array = nil
                 for string in current-array
                 do (loop for c across original-string
                          for value = (concatenate 'string string (string c))
                          do (push value next-array)
                             (push value all))
                    (setf current-array (reverse next-array)))
        finally (return (nreverse (delete-if #'(lambda (el) (< (length el) x)) all)))))

I inna wersja, nieco krótsza i wykorzystująca więcej funkcji pętli:

(defun perms (x y original-string)
  (loop repeat y
        collect (loop for string in (or (car (last sets)) (list ""))
                      append (loop for c across original-string
                                   collect (concatenate 'string string (string c)))) into sets
        finally (return (loop for set in sets
                              append (loop for el in set when (>= (length el) x) collect el)))))

Oto proste rozwiązanie rekurencyjne w języku C #:

Metoda:

public ArrayList CalculateWordPermutations(string[] letters, ArrayList words, int index)
        {
            bool finished = true;
            ArrayList newWords = new ArrayList();
            if (words.Count == 0)
            {
                foreach (string letter in letters)
                {
                    words.Add(letter);
                }
            }

            for(int j=index; j<words.Count; j++)
            {
                string word = (string)words[j];
                for(int i =0; i<letters.Length; i++)
                {
                    if(!word.Contains(letters[i]))
                    {
                        finished = false;
                        string newWord = (string)word.Clone();
                        newWord += letters[i];
                        newWords.Add(newWord);
                    }
                }
            }

            foreach (string newWord in newWords)
            {   
                words.Add(newWord);
            }

            if(finished  == false)
            {
                CalculateWordPermutations(letters, words, words.Count - newWords.Count);
            }
            return words;
        }

Powołanie:

string[] letters = new string[]{"a","b","c"};
ArrayList words = CalculateWordPermutations(letters, new ArrayList(), 0);

... a oto wersja C:

void permute(const char *s, char *out, int *used, int len, int lev)
{
    if (len == lev) {
        out[lev] = '\0';
        puts(out);
        return;
    }

    int i;
    for (i = 0; i < len; ++i) {
        if (! used[i])
            continue;

        used[i] = 1;
        out[lev] = s[i];
        permute(s, out, used, len, lev + 1);
        used[i] = 0;
    }
    return;
}

permute (ABC) -> A. nasienie (BC) -> A. nasienie [B. derma (C)] -> A. nasienie [( * B C), (C B * )] -> [( * A BC ), (B A C), (BC A * ), ( * A CB), (C A B), (CB A * )] Aby usunąć duplikaty podczas wstawiania każdego alfabetu, sprawdź, czy poprzedni ciąg kończy się tym samym alfabetem (dlaczego? - ćwiczenie)

public static void main(String[] args) {

    for (String str : permStr("ABBB")){
        System.out.println(str);
    }
}

static Vector<String> permStr(String str){

    if (str.length() == 1){
        Vector<String> ret = new Vector<String>();
        ret.add(str);
        return ret;
    }

    char start = str.charAt(0);
    Vector<String> endStrs = permStr(str.substring(1));
    Vector<String> newEndStrs = new Vector<String>();
    for (String endStr : endStrs){
        for (int j = 0; j <= endStr.length(); j++){
            if (endStr.substring(0, j).endsWith(String.valueOf(start)))
                break;
            newEndStrs.add(endStr.substring(0, j) + String.valueOf(start) + endStr.substring(j));
        }
    }
    return newEndStrs;
}

Drukuje wszystkie permutacje bez duplikatów

Rozwiązanie rekurencyjne w C ++

int main (int argc, char * const argv[]) {
        string s = "sarp";
        bool used [4];
        permute(0, "", used, s);
}

void permute(int level, string permuted, bool used [], string &original) {
    int length = original.length();

    if(level == length) { // permutation complete, display
        cout << permuted << endl;
    } else {
        for(int i=0; i<length; i++) { // try to add an unused character
            if(!used[i]) {
                used[i] = true;
                permute(level+1, original[i] + permuted, used, original); // find the permutations starting with this string
                used[i] = false;
            }
        }
}

W Perlu, jeśli chcesz ograniczyć się do małych liter, możesz to zrobić:

my @result = ("a" .. "zzzz");

Daje to wszystkie możliwe ciągi od 1 do 4 znaków z małymi literami. Zmień na wielkie litery"a" na "A"i "zzzz"na "ZZZZ".

W przypadku przypadków mieszanych staje się to znacznie trudniejsze i prawdopodobnie nie da się tego zrobić z jednym z wbudowanych operatorów Perla, takich jak ten.

Odpowiedź Ruby, która działa:

class String
  def each_char_with_index
    0.upto(size - 1) do |index|
      yield(self[index..index], index)
    end
  end
  def remove_char_at(index)
    return self[1..-1] if index == 0
    self[0..(index-1)] + self[(index+1)..-1]
  end
end

def permute(str, prefix = '')
  if str.size == 0
    puts prefix
    return
  end
  str.each_char_with_index do |char, index|
    permute(str.remove_char_at(index), prefix + char)
  end
end

# example
# permute("abc")

import java.util.*;

public class all_subsets {
    public static void main(String[] args) {
        String a = "abcd";
        for(String s: all_perm(a)) {
            System.out.println(s);
        }
    }

    public static Set<String> concat(String c, Set<String> lst) {
        HashSet<String> ret_set = new HashSet<String>();
        for(String s: lst) {
            ret_set.add(c+s);
        }
        return ret_set;
    }

    public static HashSet<String> all_perm(String a) {
        HashSet<String> set = new HashSet<String>();
        if(a.length() == 1) {
            set.add(a);
        } else {
            for(int i=0; i<a.length(); i++) {
                set.addAll(concat(a.charAt(i)+"", all_perm(a.substring(0, i)+a.substring(i+1, a.length()))));
            }
        }
        return set;
    }
}

Następująca rekurencja Java wypisuje wszystkie permutacje danego ciągu:

//call it as permut("",str);

public void permut(String str1,String str2){
    if(str2.length() != 0){
        char ch = str2.charAt(0);
        for(int i = 0; i <= str1.length();i++)
            permut(str1.substring(0,i) + ch + str1.substring(i,str1.length()),
                     str2.substring(1,str2.length()));
    }else{
    System.out.println(str1);
    }
}

Poniżej znajduje się zaktualizowana wersja powyższej metody "permut", która sprawia, że ​​n! (n silnia) mniej rekurencyjnych wywołań w porównaniu z powyższą metodą

//call it as permut("",str);

public void permut(String str1,String str2){
   if(str2.length() > 1){
       char ch = str2.charAt(0);
       for(int i = 0; i <= str1.length();i++)
          permut(str1.substring(0,i) + ch + str1.substring(i,str1.length()),
                 str2.substring(1,str2.length()));
   }else{
    char ch = str2.charAt(0);
    for(int i = 0; i <= str1.length();i++)
        System.out.println(str1.substring(0,i) + ch +    str1.substring(i,str1.length()),
                 str2.substring(1,str2.length()));
   }
}

Nie jestem pewien, dlaczego chcesz to zrobić w pierwszej kolejności. Wynikowy zbiór dla dowolnych umiarkowanie dużych wartości x i y będzie ogromny i będzie rósł wykładniczo, gdy x i / lub y będą rosły.

Powiedzmy, że twój zestaw możliwych znaków to 26 małych liter alfabetu i poprosisz aplikację o wygenerowanie wszystkich permutacji, gdzie długość = 5. Zakładając, że nie zabraknie Ci pamięci, otrzymasz 11.881.376 (tj. 26 do potęgi 5) ciągi z powrotem. Zwiększ tę długość do 6, a otrzymasz 308 915 776 strun. Te liczby stają się boleśnie duże, bardzo szybko.

Oto rozwiązanie, które stworzyłem w Javie. Musisz podać dwa argumenty czasu wykonywania (odpowiadające x i y). Baw się dobrze.

public class GeneratePermutations {
    public static void main(String[] args) {
        int lower = Integer.parseInt(args[0]);
        int upper = Integer.parseInt(args[1]);

        if (upper < lower || upper == 0 || lower == 0) {
            System.exit(0);
        }

        for (int length = lower; length <= upper; length++) {
            generate(length, "");
        }
    }

    private static void generate(int length, String partial) {
        if (length <= 0) {
            System.out.println(partial);
        } else {
            for (char c = 'a'; c <= 'z'; c++) {
                generate(length - 1, partial + c);
            }
        }
    }
}

Oto nierekurencyjna wersja, którą wymyśliłem, w javascript. Nie jest oparty na powyższym nierekurencyjnym Knutha, chociaż ma pewne podobieństwa w zamianie elementów. Sprawdziłem jego poprawność dla tablic wejściowych do 8 elementów.

Szybką optymalizacją byłoby przygotowanie outtablicy do lotu i unikaniepush() .

Podstawowa idea to:

1. Mając jedną tablicę źródłową, wygeneruj pierwszy nowy zestaw tablic, które zamieniają pierwszy element z każdym kolejnym elementem po kolei, za każdym razem pozostawiając pozostałe elementy niezakłócone. np .: podane 1234, wygeneruj 1234, 2134, 3214, 4231.

2. Użyj każdej tablicy z poprzedniego przebiegu jako ziarna dla nowego przebiegu, ale zamiast zamieniać pierwszy element, zamień drugi element z każdym kolejnym elementem. Tym razem nie dołączaj oryginalnej tablicy do danych wyjściowych.

3. Powtarzaj krok 2, aż skończysz.

Oto przykładowy kod:

function oxe_perm(src, depth, index)
{
    var perm = src.slice();     // duplicates src.
    perm = perm.split("");
    perm[depth] = src[index];
    perm[index] = src[depth];
    perm = perm.join("");
    return perm;
}

function oxe_permutations(src)
{
    out = new Array();

    out.push(src);

    for (depth = 0; depth < src.length; depth++) {
        var numInPreviousPass = out.length;
        for (var m = 0; m < numInPreviousPass; ++m) {
            for (var n = depth + 1; n < src.length; ++n) {
                out.push(oxe_perm(out[m], depth, n));
            }
        }
    }

    return out;
}

W rubinie:

str = "a"
100_000_000.times {puts str.next!}

Jest to dość szybkie, ale zajmie to trochę czasu =). Oczywiście możesz zacząć od „aaaaaaaa”, jeśli krótkie struny cię nie interesują.

Mogłem jednak źle zinterpretować rzeczywiste pytanie - w jednym z postów brzmiało to tak, jakbyś potrzebował brutalnej biblioteki strun, ale w głównym pytaniu brzmi to tak, jakbyś musiał permutować konkretny ciąg.

Twój problem jest nieco podobny do tego: http://beust.com/weblog/archives/000491.html ( wypisz wszystkie liczby całkowite, w których żadna z cyfr się nie powtarza, co spowodowało, że wiele języków go rozwiązało, z ocaml, który używa permutacji, i jakiś java, używając jeszcze innego rozwiązania).

Potrzebowałem tego dzisiaj i chociaż odpowiedzi już udzielone wskazały mi właściwy kierunek, nie były one tym, czego chciałem.

Oto implementacja wykorzystująca metodę Heapa. Długość tablicy musi wynosić co najmniej 3, a ze względów praktycznych nie więcej niż 10, w zależności od tego, co chcesz zrobić, cierpliwości i szybkości zegara.

Przed wprowadzeniem pętli, zainicjować Perm(1 To N)z pierwszym permutacji, Stack(3 To N)z zer * oraz Levelz 2**. Na końcu wywołania pętli NextPerm, które zwróci false, gdy skończymy.

* VB zrobi to za Ciebie.

** Możesz trochę zmienić NextPerm, aby było to niepotrzebne, ale jest to wyraźniejsze w ten sposób.

Option Explicit

Function NextPerm(Perm() As Long, Stack() As Long, Level As Long) As Boolean
Dim N As Long
If Level = 2 Then
    Swap Perm(1), Perm(2)
    Level = 3
Else
    While Stack(Level) = Level - 1
        Stack(Level) = 0
        If Level = UBound(Stack) Then Exit Function
        Level = Level + 1
    Wend
    Stack(Level) = Stack(Level) + 1
    If Level And 1 Then N = 1 Else N = Stack(Level)
    Swap Perm(N), Perm(Level)
    Level = 2
End If
NextPerm = True
End Function

Sub Swap(A As Long, B As Long)
A = A Xor B
B = A Xor B
A = A Xor B
End Sub

'This is just for testing.
Private Sub Form_Paint()
Const Max = 8
Dim A(1 To Max) As Long, I As Long
Dim S(3 To Max) As Long, J As Long
Dim Test As New Collection, T As String
For I = 1 To UBound(A)
    A(I) = I
Next
Cls
ScaleLeft = 0
J = 2
Do
    If CurrentY + TextHeight("0") > ScaleHeight Then
        ScaleLeft = ScaleLeft - TextWidth(" 0 ") * (UBound(A) + 1)
        CurrentY = 0
        CurrentX = 0
    End If
    T = vbNullString
    For I = 1 To UBound(A)
        Print A(I);
        T = T & Hex(A(I))
    Next
    Print
    Test.Add Null, T
Loop While NextPerm(A, S, J)
J = 1
For I = 2 To UBound(A)
    J = J * I
Next
If J <> Test.Count Then Stop
End Sub

Inne metody są opisane przez różnych autorów. Knuth opisuje dwa, jeden daje porządek leksykalny, ale jest złożony i powolny, drugi jest znany jako metoda prostych zmian. Jie Gao i Dianjun Wang również napisali interesujący artykuł.

Ten kod w Pythonie, wywołany z allowed_charactersustawieniem na [0,1]i maksymalnie 4 znakami, wygeneruje 2 ^ 4 wyników:

['0000', '0001', '0010', '0011', '0100', '0101', '0110', '0111', '1000', '1001', '1010', '1011', '1100', '1101', '1110', '1111']

def generate_permutations(chars = 4) :

#modify if in need!
    allowed_chars = [
        '0',
        '1',
    ]

    status = []
    for tmp in range(chars) :
        status.append(0)

    last_char = len(allowed_chars)

    rows = []
    for x in xrange(last_char ** chars) :
        rows.append("")
        for y in range(chars - 1 , -1, -1) :
            key = status[y]
            rows[x] = allowed_chars[key] + rows[x]

        for pos in range(chars - 1, -1, -1) :
            if(status[pos] == last_char - 1) :
                status[pos] = 0
            else :
                status[pos] += 1
                break;

    return rows

import sys


print generate_permutations()

Mam nadzieję, że to ci się przyda. Działa z każdym znakiem, nie tylko cyframi

Oto łącze, które opisuje, jak wydrukować permutacje ciągu. http://nipun-linuxtips.blogspot.in/2012/11/print-all-permutations-of-characters-in.html

Chociaż to nie odpowiada dokładnie na twoje pytanie, oto jeden sposób na wygenerowanie każdej permutacji liter z wielu ciągów o tej samej długości: np. Jeśli twoje słowa to „kawa”, „joomla” i „moodle”, możesz oczekuj wyników, takich jak „coodle”, „joodee”, „joffle” itp.

Zasadniczo liczba kombinacji to (liczba słów) do potęgi (liczba liter na słowo). Wybierz więc losową liczbę z przedziału od 0 do liczby kombinacji - 1, zamień tę liczbę na podstawę (liczbę słów), a następnie użyj każdej cyfry tej liczby jako wskaźnika, z którego słowa należy wziąć następną literę.

np. w powyższym przykładzie. 3 słowa, 6 liter = 729 kombinacji. Wybierz losową liczbę: 465. Konwertuj na podstawę 3: 122020. Weź pierwszą literę ze słowa 1, drugą ze słowa 2, trzecią ze słowa 2, czwartą ze słowa 0 ... a otrzymasz ... „joofle”.

Jeśli chcesz uzyskać wszystkie permutacje, po prostu zapętlaj od 0 do 728. Oczywiście, jeśli wybierasz tylko jedną losową wartość, znacznie prostszym, mniej zagmatwanym sposobem byłoby zapętlenie nad literami. Ta metoda pozwala uniknąć rekurencji, jeśli chcesz mieć wszystkie permutacje, a także sprawia, że ​​wyglądasz tak, jakbyś znał matematykę ^(tm) !

Jeśli liczba kombinacji jest nadmierna, możesz podzielić ją na serię mniejszych słów i połączyć je na końcu.

c # iteracyjny:

public List<string> Permutations(char[] chars)
    {
        List<string> words = new List<string>();
        words.Add(chars[0].ToString());
        for (int i = 1; i < chars.Length; ++i)
        {
            int currLen = words.Count;
            for (int j = 0; j < currLen; ++j)
            {
                var w = words[j];
                for (int k = 0; k <= w.Length; ++k)
                {
                    var nstr = w.Insert(k, chars[i].ToString());
                    if (k == 0)
                        words[j] = nstr;
                    else
                        words.Add(nstr);
                }
            }
        }
        return words;
    }

def gen( x,y,list): #to generate all strings inserting y at different positions
list = []
list.append( y+x )
for i in range( len(x) ):
    list.append( func(x,0,i) + y + func(x,i+1,len(x)-1) )
return list 

def func( x,i,j ): #returns x[i..j]
z = '' 
for i in range(i,j+1):
    z = z+x[i]
return z 

def perm( x , length , list ): #perm function
if length == 1 : # base case
    list.append( x[len(x)-1] )
    return list 
else:
    lists = perm( x , length-1 ,list )
    lists_temp = lists #temporarily storing the list 
    lists = []
    for i in range( len(lists_temp) ) :
        list_temp = gen(lists_temp[i],x[length-2],lists)
        lists += list_temp 
    return lists

def permutation(str)
  posibilities = []
  str.split('').each do |char|
    if posibilities.size == 0
      posibilities[0] = char.downcase
      posibilities[1] = char.upcase
    else
      posibilities_count = posibilities.length
      posibilities = posibilities + posibilities
      posibilities_count.times do |i|
        posibilities[i] += char.downcase
        posibilities[i+posibilities_count] += char.upcase
      end
    end
  end
  posibilities
end

Oto moje podejście do wersji nierekurencyjnej

Rozwiązanie pytoniczne:

from itertools import permutations
s = 'ABCDEF'
p = [''.join(x) for x in permutations(s)]

Oto eleganckie, nierekurencyjne rozwiązanie O (n!):

public static StringBuilder[] permutations(String s) {
        if (s.length() == 0)
            return null;
        int length = fact(s.length());
        StringBuilder[] sb = new StringBuilder[length];
        for (int i = 0; i < length; i++) {
            sb[i] = new StringBuilder();
        }
        for (int i = 0; i < s.length(); i++) {
            char ch = s.charAt(i);
            int times = length / (i + 1);
            for (int j = 0; j < times; j++) {
                for (int k = 0; k < length / times; k++) {
                    sb[j * length / times + k].insert(k, ch);
                }
            }
        }
        return sb;
    }