Co wskazuje na kształt klina wykresu PCA?

W swojej pracy w autoencoders do klasyfikacji tekst Hinton i Salakhutdinov wykazały wykres wytwarzanego przez 2 wymiarowe LSA (co jest ściśle związane z PCA) .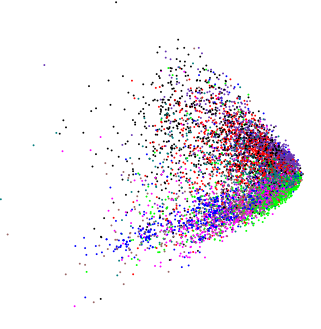

Stosując PCA do absolutnie różnych nieco nieco wymiarowych danych, otrzymałem podobnie wyglądający wykres: (z wyjątkiem tego przypadku naprawdę chciałem wiedzieć, czy jest jakaś struktura wewnętrzna).

Jeśli wprowadzimy losowe dane do PCA, otrzymamy kroplę w kształcie dysku, więc ten kształt w kształcie klina nie jest losowy. Czy to samo coś znaczy?

Zakładając, że zmienne są dodatnie lub nieujemne, krawędzie krawędzi są tylko punktami, powyżej których dane stałyby się odpowiednio 0 lub ujemne. Ponieważ takie rzeczywiste dane są zwykle wypaczone, widzimy większą gęstość punktów na dolnym końcu ich rozkładu, a zatem większą gęstość w „punkcie” klina.

Mówiąc bardziej ogólnie, PCA to po prostu obrót danych, a ograniczenia na tych danych będą ogólnie widoczne w głównych składnikach w taki sam sposób, jak pokazano w pytaniu.

Oto przykład wykorzystujący kilka zmiennych logarytmicznych o rozkładzie normalnym:

library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

W zależności od rotacji sugerowanej przez dwa pierwsze komputery PC możesz zobaczyć klin lub nieco inną wersję, pokazaną tutaj w 3D za pomocą ( ordirgl()zamiast plot())

Tutaj w 3d widzimy wiele kolców wystających z masy centralnej.

Dla losowych zmiennych Gaussa ($X_i \sim \mathcal(N)(\mu = 0, \sigma = 1)$), gdzie każdy ma tę samą średnią i wariancję, widzimy sferę punktów

set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")

A dla jednolitych dodatnich zmiennych losowych widzimy sześcian

set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")

Zauważ, że tutaj dla ilustracji pokazuję mundur używając tylko 3 zmiennych losowych, stąd punkty opisują sześcian w 3d. Przy wyższych wymiarach / większej liczbie zmiennych nie możemy idealnie przedstawić hipersześcianu 5d w 3d, a zatem wyraźny kształt „sześcianu” ulega nieco zniekształceniu. Podobne problemy wpływają na inne pokazane przykłady, ale nadal łatwo zauważyć ograniczenia w tych przykładach.

Dla twoich danych transformacja logiczna zmiennych przed PCA pociągnie za sobą ogony i rozciągnie zbite dane, tak jak możesz użyć takiej transformacji w regresji liniowej.

Inne kształty mogą pojawiać się na wykresach PCA; jeden taki kształt jest artefaktem reprezentacji metrycznej zachowanym w PCA i jest znany jako podkowa . W przypadku danych o długim lub dominującym gradiencie (próbki ułożone wzdłuż jednego wymiaru ze zmiennymi zwiększającymi się od 0 do maksimum, a następnie zmniejszającymi się ponownie do 0 wzdłuż części danych, są dobrze znane z generowania takich artefaktów.

ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
                 Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
                 Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
        ylab = "Abundance", xlab = "Sites")

co tworzy ekstremalną podkowę, w której punkty na końcach osi wyginają się z powrotem w środek.