Zastanawiam się, czy istnieje dobry przykład łatwego do zrozumienia problemu NP-Hard, który nie jest NP-Complete i nie jest nierozstrzygalny?
Na przykład problem zatrzymania jest NP-trudny, a nie NP-kompletny, ale jest nierozstrzygalny.
Uważam, że oznacza to, że problem można zweryfikować, ale nie w czasie wielomianowym. (Proszę poprawić to oświadczenie, jeśli tak nie jest).

Odpowiedzi:
Według niedeterministycznej wersji twierdzenia o hierarchii czasowej mamyNP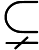 NEXP
NEXP , gdzie NEXP jest klasą problemów możliwych do rozwiązania w niedeterministycznym czasie wykładniczym. Dlatego wystarczy rozważyć każdy problem, który to NP -hard and in NEXP , ale nie w NP . Na przykład, możemy rozważyć każdy problem NEXP , taki jak
3-kolorowalność wykresów opisanych zwięzłymi obwodami - lub innym problemem NP-zupełnym na wykresach - gdzie „zwięzły obwód” jest formatem reprezentującym bardzo duże wykresy na wejściu: zamiast wyraźnej reprezentacji wykresu, np. Listami przyległości, zamiast tego udostępniamy obwód obliczający jakąś funkcję

























(Nie-) równoważność dwóch wyrażeń regularnych, w których gwiazdę Kleene zastępuje się kwadratem (powtarzanie pod-wzoru dokładnie dwa razy, a nie zero lub więcej razy), i gdzie pytamy, czy dwa takie wyrażenia regularne reprezentują różne zestawy ciągów.
Zauważ, że w tym drugim przypadku, jeśli weźmiemy pod uwagę wyrażenia regularne, takie jak gwiazda Kleene, wynikającym z tego problemem jest : ponieważ mamy , to wciąż jest rozstrzygalny problem, którym jest -trwały, a nie .EXPSPACE NP NEXP
NEXP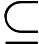 EXPSPACE
EXPSPACE NP NP
źródło
Zastrzeżenie: Ta odpowiedź opiera się na założeniu, że , hipoteza, w którą większość naukowców mocno wierzy, ale musimy ją jeszcze udowodnić. Oznacza to, że istnieje możliwość, że problemy te znajdują się w a zatem także -complete.












Powiedziałbym, że najprostsze z nich to prawdziwie skwantyfikowana formuła logiczna i uogólniona geografia , oba -kompletne.





TQBF otrzymuje skwantyfikowaną formułę logiczną, sprawdź , czy formuła jest prawdziwa, tj. Formuły w formularzu jest fałszem, ponieważ ustawienie na false daje fałszywe wyrażenie.
















Geografia uogólniona to fajna gra (patrz łańcuch słów ), w której masz listę ciągów znaków (np. Nazwy miast), a Gracz 1 zaczyna się od wypowiedzenia imienia, a Gracz 2 odpowiada imieniem rozpoczynającym się na literę, na której poprzednia nazwa się kończyła. Potem jest kolej Gracza 1., aż ktoś utknie (ta gra jest zalecana do grania w gry alkoholowe, w których obiektami są zespoły / artyści, filmy, miasta, stolice, sławni matematycy lub cokolwiek płynie łodzią. Ten, który nie może odpowiedzieć w rozsądnym czasie) oczywiście trzeba pić). Problem formalny jest sformułowany jako pytanie „czy Gracz 1 ma strategię wygrywającą” .
źródło