Twierdzenie Ladnera dobrze wie, że jeśli , wówczas istnieje nieskończenie wiele pośrednich ( ). Istnieją również naturalni kandydaci do tego statusu, tacy jak Graph Isomorphism i wiele innych, patrz Problemy między P i NPC . Niemniej jednak ogromna większość w tłumie znanych jest znana z lub . Tylko niewielka część z nich pozostaje kandydatem do . Innymi słowy, jeśli losowo wybierzemy naturalnyN P N P I natural N P P N P C N P I N P N P I -problem wśród znanych, mamy bardzo małą szansę na wybranie kandydata . Czy jest jakieś wytłumaczenie tego zjawiska?
Mógłbym wymyślić 3 możliwe wyjaśnienia, bardziej filozoficzne:
Powodem posiadania tak małej frakcji naturalnych kandydatów jest to, że ostatecznie okaże się pusty. Wiem, że oznacza to , więc jest bardzo mało prawdopodobne. Niemniej jednak nadal można argumentować (choć nie jestem jednym z nich), że rzadkość naturalnych problemów jest obserwacją empiryczną, która wydaje się w rzeczywistości wspierać , w przeciwieństwie do większości innych obserwacji.N P I P = N P N P I P = N P
Małe „natural- ” reprezentuje rodzaj ostrego przejścia fazowego między łatwymi i trudnymi problemami. Najwyraźniej znaczące, naturalne problemy algorytmiczne zachowują się w taki sposób, że są albo łatwe, albo trudne, przejście jest wąskie (ale nadal istnieje).
Argument z 2 może być doprowadzony do skrajności: w końcu wszystkie problemy w „natural- ” zostaną wprowadzone do , a jednak , więc . Oznaczałoby to, że wszystkie pozostałe problemy wP ∪ N P C P ≠ N P N P I ≠ ∅ N P Isą „nienaturalne” (wymyślone, bez sensu życia). Interpretacją tego może być to, że naturalne problemy są albo łatwe, albo trudne; przejście jest tylko logiczną konstrukcją, bez znaczenia „fizycznego”. Jest to nieco podobne do przypadku liczb niewymiernych, które są całkowicie logiczne, ale nie powstają jako zmierzona wartość jakiejkolwiek wielkości fizycznej. Jako takie nie pochodzą one z rzeczywistości fizycznej, są raczej w „logicznym zamknięciu” tej rzeczywistości.
Które wyjaśnienie najbardziej ci odpowiada, czy możesz zasugerować inne?
źródło




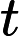
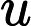





Odpowiedzi:
Jak zauważyli inni, dyskusyjne jest, w jakim stopniu rzecz, którą próbujesz wyjaśnić, jest prawdziwa. Można argumentować, że w latach 60. i 70. informatycy teoretyczni byli po prostu bardziej zainteresowani rodzajem problemów, które okazały się albo w P, albo w NP-zupełnym. Dzisiaj, ze względu na wzrost złożoności - kryptografii teoretycznej, obliczeń kwantowych, sieci itp. - a także prostego faktu, że kompletność NP stała się tak dobrze zrozumiała - coraz bardziej interesujemy się rodzaje problemów, które okazują się być pośrednimi NP.
Mimo to można zapytać: w takim stopniu, w jakim rzecz jest prawdziwa - to znaczy w takim stopniu, że tak wiele naturalnych problemów z wyszukiwaniem i optymalizacją „przyciąga” albo być NP-zupełnym, albo też w P --- w tym zakresie , dlaczego jest to prawda? Tutaj myślę, że można uzyskać wiele intuicji, patrząc na wcześniejsze zjawisko od obliczalności: że tak wiele naturalnych modeli obliczeń „zatrzaskuje się” aż do ukończenia Turinga. W takim przypadku powiem, że wyjaśnienie jest takie, że gdy masz kilka podstawowych składników --- pamięć do odczytu / zapisu, pętle, warunki warunkowe itp. - trudno jest tego uniknąćmożliwość symulowania maszyny Turinga, a tym samym ukończenie Turinga. W podobny sposób, gdy problem wyszukiwania lub optymalizacji składa się z kilku podstawowych elementów --- co najważniejsze, możliwość konstruowania „gadżetów” naśladujących bramki logiczne, takie jak AND, OR i NOT --- trudno jest uniknąć do kodowania SAT i dlatego jest NP-kompletny.
Tak jak lubię o tym myśleć, problemy takie jak SAT wywierają potężne „przyciąganie grawitacyjne” na wszystkie inne problemy obliczeniowe w ich sąsiedztwie, powodując, że chcą „złapać” się na ukończenie NP również. Tak więc normalnie nie wymaga nawet specjalnego wyjaśnienia, gdy kolejny problem ulega temu pociągnięciu! Bardziej uderzające i wymagające wyjaśnienia jest to, że (pozornie) trudny problem NP ma jakąś właściwość, która pozwala mu oprzeć się grawitacyjnemu oddziaływaniu SAT. Następnie chcemy wiedzieć: co to za właściwość? Dlaczego nie możesz zagrać w zwykłą sztuczkę NP-zupełności dotyczącą tego problemu, polegającą na tworzeniu gadżetów kodujących logiczne bramki logiczne? W ostatniej odpowiedzi na CS.SE stworzyłem listę typowych odpowiedzi na to pytanie, ale (jak już zauważył inny komentator) istnieją inne możliwe odpowiedzi, które przeoczyłem.
źródło
Wiele naturalnych problemów można wyrazić jako problemy związane z ograniczeniami, a dla CSP istnieją twierdzenia o dychotomii.
źródło
Po prostu żart: po zastanowieniu się nad „przyciąganiem grawitacyjnym SAT” w miłej odpowiedzi Scotta Aaronsona, przyszła mi do głowy inna metafora: kanapka 3-SAT 2-SAT !
... ale nie wiem, czy kanapkę można napełnić naturalnymi składnikami (jednak zauważyłem, że można ją wypełnić niektórymi - Sos SAT [1], jeśli hipoteza czasu wykładniczego jest prawdziwa) :-D
Innym wynikiem w [1] jest to, że nie można go wypełnić .







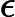




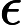


[1] Yunlei Zhao, Xiaotie Deng, CH Lee, Hong Zhu, -SAT i jego właściwości







źródło
Referencje :
1- M. Grohe. Złożoność problemów homomorfizmu i satysfakcji z ograniczeń widziane z drugiej strony. Journal of the ACM, 54 (1), art. 1, 2007
2 - Peter Jonsson, Victor Lagerkvist i Gustav Nordh. Dmuchanie dziur w różnych aspektach problemów obliczeniowych, z zastosowaniami do spełnienia ograniczenia. W materiałach z 19. Międzynarodowej Konferencji nt. Zasad i Praktyki Programowania Ograniczeń (CP-2013). 2013.
źródło
Oto bajka o strukturze Złotowłosa problemów pośrednich NP. (Ostrzeżenie: ta historia może być użytecznym błędem do generowania i testowania potencjalnych hipotez, ale nie ma być naukowo rygorystyczna. Opiera się na jednej części wykładniczej hipotezy czasowej, odrobinie magii złożoności Kołmogorowa, niektórych fragmentów zapożyczonych z teorii SAT rozwiązywanie, a heurystyczna trichotomia Terence'a Tao w przypadku problemów. Spożywać na własne ryzyko, jak w przypadku wszystkich wymyślonych mikstur dotyczących matematyki).
Jeśli prawie wszystkie wystąpienia problemu w NP mają wysoce ustrukturyzowaną strukturę, wówczas problem dotyczy w rzeczywistości P. W ten sposób prawie wszystkie wystąpienia zawierają dużo nadmiarowości, a algorytm wielomianowy dla problemu jest sposobem na wykluczenie nadmiarowości. Można sobie nawet wyobrazić, że każdy problem w P można uzyskać, biorąc jakiś problem w EXP i dodając pewną ustrukturyzowaną redundancję, poprzez jakąś formę wypełniania (niekoniecznie zwykłego rodzaju). Gdyby tak było, to algorytm czasu wielomianowego mógłby być postrzegany jako skuteczny sposób na cofnięcie tego wypełnienia.
Jeśli jest wystarczająco dużo instancji, które nie są ustrukturyzowane, tworząc „rdzeń twardości”, problem jest NP-zupełny.
Jeśli jednak ten „rdzeń twardości” jest zbyt rzadki, wówczas ma tylko miejsce na reprezentację części SAT, więc problem występuje w P lub NP-pośrednim. (Ten argument jest istotą twierdzenia Ladnera). Aby użyć analogii Scotta, „rdzeń twardości” wywiera grawitacyjny wpływ na problem, w kierunku jego zupełności NP. Instancje w „rdzeniu twardości” nie zawierają zbyt dużej nadmiarowości, a jedynym realistycznym algorytmem, który działa dla wszystkich tych instancji, jest wyszukiwanie metodą brute force (oczywiście, jeśli jest ich tylko wiele, to działa również wyszukiwanie tabel).
Z tej perspektywy problemy NP-pośrednie powinny być rzadkie w praktyce, ponieważ wymagają one równowagi Goldilocks między instancjami, które są ustrukturyzowane i nieustrukturyzowane. Instancje powinny mieć wystarczającą redundancję, aby były częściowo podatne na algorytm, ale powinno wystarczyć rdzeń twardości, aby problem nie występował w P.
Można opowiedzieć jeszcze prostszą (i zabawną, ale także potencjalnie bardziej mylącą) historię opartą na łamigłówkach. Z kilkoma ograniczeniami można zmusić do przeprowadzenia wielu poszukiwań, na przykład NxN Sudoku jest NP-kompletny. Rozważmy teraz prośbę o rozwiązanie wielu małych łamigłówek za jednym razem, za jednym razem (np. Wiele Sudokusów 9x9). Wymagany czas będzie mniej więcej liniowy w liczbie puzzli w każdym przypadku, a ten problem jest następnie w P. W przypadku problemów pośrednich można pomyśleć, że każde wystąpienie jest dużą (ale niezbyt dużą) liczbą Sudokusów w dużej (ale niezbyt duże) siatki. Powodem, dla którego nie obserwujemy wielu takich problemów, jest to, że pozowanie i rozwiązywanie ich byłyby ponure!
źródło
źródło