Jak myśleć o bramce Z w kuli Blocha?

11

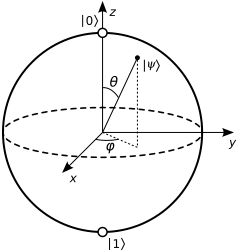
Jestem zdezorientowany, jak rozumieć bramę w kuli Blocha. $Z$

Biorąc pod uwagę macierz zrozumiałe jest, że i . $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ $Z|0\rangle = |0\rangle$ $Z|1\rangle = -|1\rangle$

Wyjaśniono tutaj , że jest brama obrót wokół osi. Więc jak mam rozumieć ? Ponieważ jest biegun południowy, czuję, że to jest naturalne, aby myśleć, że obrót wokół osi nic nie robi. $Z$ $\pi$ $Z$ $Z|1\rangle = -|1\rangle$ $|1\rangle$ $\pi$ $Z$

quantum-gate bloch-sphere Bick
źródło

7

Sposób myślenia o kuli Blocha polega na matrycy gęstości dla stanu. $Z$ działając albo $|0\rangle\langle 0|$ lub $|1\rangle\langle 1|$ nic nie robi, jak to ma miejsce w przypadku macierzy diagonalnej gęstości. Aby zobaczyć efekt obrotu, musisz spojrzeć na to, jak zmienia się dowolna macierz gęstości nieedagonalnej $Z$ , Jak na przykład $|+\rangle\langle +|$ .

DaftWullie
źródło

8

$|1\rangle$ i $-|1\rangle$ są przypisane do tego samego punktu na sferze Blocha, ponieważ są równe fazie globalnej . Algebraicznie: $|1\rangle \equiv -|1\rangle$ gdzie $\equiv$ oznacza „równa się fazie globalnej”. Oznacza to, że jest kilka $\theta$ takie, że $-|1\rangle = e^{i \theta} |1\rangle$ .

Tym, co was dezorientuje, jest to, że pomimo tego $|0\rangle \equiv Z |0\rangle$ i $|1\rangle \equiv Z |1\rangle$ , nie dotyczy to liniowych kombinacji tych dwóch. Na przykład, $Z |+\rangle \not\equiv Z |+\rangle$ nawet jeśli $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$ .

Craig Gidney
źródło

2

Zgodnie z Wikipedią możemy napisać dowolny stan czysty jako

| ψ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{θ}{2}) | 1 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

Gdzie $\theta$ i $\phi$ są kąty na kuli Blocha:

Prawie każdy punkt na powierzchni (tj. Stan czysty) ma unikalną reprezentację pod względem kątów, z wyjątkiem biegunów. Podobnie jak na Ziemi, Biegun Południowy nie ma dobrze określonej długości geograficznej (każda długość geograficzna działa tak samo), dla $|1 \rangle$ podać dowolną fazę $\phi$ oznacza to samo. „Szerokość geograficzna” $\theta$ jest tutaj $\pi$ , podłączmy to do równania:

| 1 ⟩ = \cos (\frac{π}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{π}{2}) | 1 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + e^{i ϕ} | 1 ⟩

$= 0 + e^{i \phi} |1 \rangle$

Jeśli znasz tożsamość Eulera, prawdopodobnie rozpoznasz $e^{i \phi}$ jako obrót w płaszczyźnie złożonej. W szczególności, ponieważ $Z$ jest rotacją dla $\phi = \pi$ , otrzymujemy sławę $e^{i \pi} = -1$ , wreszcie przybywając do $|1 \rangle = - |1 \rangle$ .

Norrius
źródło

1

To jest źle. Pisanie

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$ wprowadza w błąd: są to stany równoważne, ponieważ różnią się tylko fazą globalną, ale to nie znaczy, że wektory stanu są takie same. Uzyskujesz ten wynik, ponieważ zakładasz, że nastąpi bijection między wektorami stanu i punktami na sferze Blocha, co nie jest prawdą. Bijection stoi pomiędzy punktami na kuli Blocha a stanami opisanymi jako macierze gęstości

glS

@glS Dzięki,

1 = - 1

$1=-1$ wynika z tego, że wydawało się podejrzane. Czy sensowne jest poprawienie tej odpowiedzi z Twojej perspektywy, czy też jest to beznadziejnie złe?

Norrius

to jest twój telefon =). Myślę, że poprawną odpowiedzią jest ta, którą podał DaftWullie (uważam, że pytający miał podobne nieporozumienie jak w twojej odpowiedzi). Nie widzę wiele do powiedzenia na temat tego pytania

glS

Jak myśleć o bramce Z w kuli Blocha?

Odpowiedzi: